30年悬而未决的数学难题就这样被AI证明了?!
此时此刻,(前推特)正在刮起一股讨论之风——
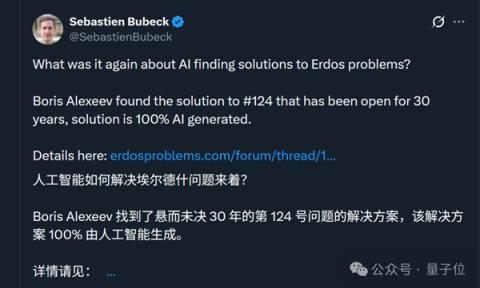
来自Harmonic的数学AI模型独立证明了Erd?s问题#124,而这个问题已经被数学家无奈搁置了近30年。

微软前AI副总裁、目前在OpenAI研究AGI的Sebastien Bubeck激动分享了这一消息,并表示:
该解决方案100%由AI生成,总计耗时6小时。
甚至连陶哲轩这样的顶尖数学家也跑来围观讨论,他在对比了Gemini和ChatGPT的深度研究工具后发现,Harmonic模型对该问题的证明表现更佳。

所以这到底是一个怎样的问题?Harmonic模型又是如何“大显神功”?
咱接着瞧——
AI证明了Erd?s问题#124简易版
首先需要提醒,在听完各路大神讨论后,我们才意识到——
原来Harmonic模型所证明的并非原版Erd?s问题#124,而是一个简易版本。
Erd?s问题#124需要提供的证明如下:

通俗理解即为:
假设你有k个不同的“进制生成器”,分别对应数字d1, d2, …, dk。
游戏规则为:1)你可以从每个生成器产生的数字列表中,至多挑选一个;2)然后把你挑出来的所有这些数字加起来;3)最后看能不能正好凑出你的目标数。
这个问题的核心就是——
只要你的这套“进制生成器”满足一个特定的条件,即1/(d1-1) +1/(d2-1)+…+1/(dk-1)≥ 1,那么是不是所有的、足够大的整数,都能用这种规则凑出来?
截至目前,这个问题取得的进展可以概括为:
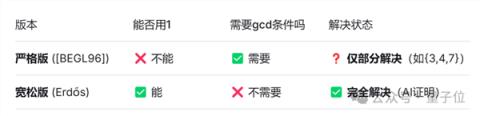
就是说,这个问题在几十年里逐渐演变为难易两个版本。
在原版[BEGL96]中,挑战者不允许使用数字1且需要额外满足gcd条件(各个进制之间没有“重复周期”),最终仅发现,对于特定集合 {3, 4, 7}猜想成立。
而当条件放宽之后(允许使用数字1且不需要额外满足gcd条件),Harmonic模型成功证明只要满足上述特定条件,就一定能凑出所有大整数,而且相关证明已经得到Lean形式化验证。
Harmonic模型的证明方案如下,大佬们纷纷表示,这个方案出乎意料的简单。

不过,此次用Harmonic模型证明#124简易版的BorisAlexeev也补充道:
在“形式化猜想”项目中,原本有这个猜想的正式数学表述。但里面有个笔误:注释里写的是≥1,而对应的Lean程序代码里写的却是=1。这个错误让原表述的条件变弱了,即只覆盖了等于1的情况,而漏掉了大于1的情况。
因此,我修正了这个错误,并删除了原表述中我认为不必要的部分。最终,AI成功证明了这个更简洁、更准确的版本。
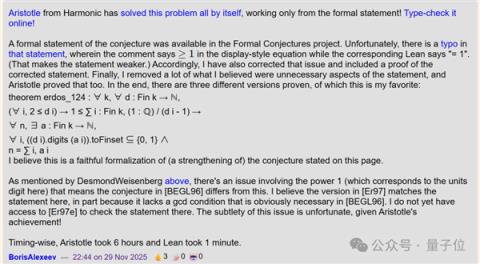
总结起来就是,Harmonic证明了问题#124的简易版本,而困难版本仍悬而未决。
“Vibe证明时代已经到来”
尽管如此,大佬们还是对AI模型证明数学难题的潜力纷纷给予了肯定。
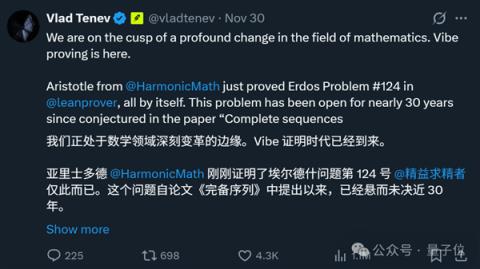
而参考编程领域的Vibe Coding概念(最早由AI大神卡帕西提出),Harmonic联创兼CEO激动表示:
我们正处于数学领域深刻变革的边缘,Vibe证明时代已经到来。
顺着他的发言,我们也去扒了扒Harmonic模型背后的出品方,毕竟在陶哲轩眼中它这次可是战胜了ChatGPT和Gemini。
根据公开资料,其背后公司名为Harmonic,目标也相当明确:
打造世界上最先进的数学推理引擎。

两位联创分别为Tudor Achim和Vlad Tenev。
CEO Tudor Achim,拥有卡内基梅隆大学计算机科学学士学位,同时也在斯坦福大学攻读计算机科学PhD,不过现处于“on leave”状态。
2023年,他和Vlad Tenev共同创办了Harmonic,当时想打造世界上最先进的推理引擎。
更早之前,他还在一家自动驾驶辅助系统开发公司(Helm.ai)担任联创和CTO。

执行主席Vlad Tenev,拥有斯坦福大学数学学士学位和加州大学洛杉矶分校数学硕士学位。
除了在Harmonic担任联创和执行主席,他目前还同时在金融公司Robinhood Markets兼任CEO。

根据官网公开资料,Harmonic在大约一周前完成了1.2亿美元(约合人民币8.5亿)C轮融资。
本轮融资由Ribbit Capital领投,估值达到14.5亿美元(约合人民币103亿)。
Harmonic的旗舰模型就是本次用到的Aristotle模型(也有叫“亚里士多德”的),据悉它是第一个在2025年国际数学奥林匹克竞赛中给出其中五道题形式化验证解决方案的模型。
Aristotle在保证准确性和消除幻觉的同时,达到了金牌级别的表现。
据Vlad Tenev透露,这次用的Aristotle进行了一些更新,具有更强大的推理能力和自然语言界面。
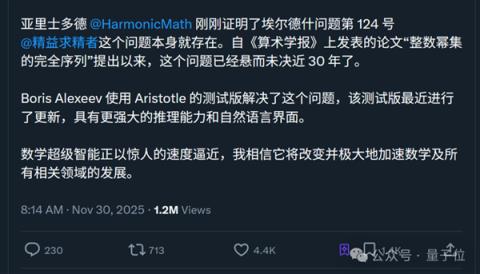
可以预见,随着AI解决复杂数学问题的能力不断突破,越来越多曾被“束之高阁”的百年难题将重见天日,并有望被逐一攻克。
Anyway,AI浪潮之下,开弓已无回头箭。
参考链接:
[1]https://x.com/i/trending/1994986636623724980
[2]https://www.erdosproblems.com/forum/thread/124#post-1892
[3]https://x.com/thomasfbloom/status/1995094668879462466
本文转载于快科技,文中观点仅代表作者个人看法,本站只做信息存储
本文来自于网络或用户投稿,本站仅供信息存储,阅读前请先查看【免责声明】,若本文侵犯了原著者的合法权益,可联系我们进行处理。本文链接:https://trustany.com/post/18849.html